MCMC Properties and Diagnostics

Author

Dr. Alexander Fisher

View libraries used in these notes 
library(tidyverse)

Practice example

As in the example from lab here, let \(y\) be the mercury concentration (ppm) of a bass fish and let \(x\) be the weight of the fish (kg). This time, our model will be:

\[ \begin{aligned} Y_i | \theta_1, \theta_2 &\sim N(\theta_1 + \theta_2 x_i, 1)\\ \theta_1, \theta_2 &\sim \text{ iid }N(0, 10) \end{aligned} \]

bass = read_csv("https://sta360-fa24.github.io/data/bass.csv")
y = bass$mercury
x = bass$weight

Sample from the posterior \(p(\theta_1, \theta_2 | y_1, \ldots, y_n, x_1, \ldots, x_n)\) using the Metropolis algorithm.

logLikelihood = function(theta1, theta2) {
  mu = theta1 + (theta2 * x)
  sum(dnorm(y, mu, 1, log = TRUE))
}

logPrior = function(theta1, theta2) {
  dnorm(theta1, 0, sqrt(10), log = TRUE) + 
    dnorm(theta2, 0, sqrt(10), log = TRUE)
}

logPosterior = function(theta1, theta2) {
  logLikelihood(theta1, theta2) + logPrior(theta1, theta2)
}


THETA1 = NULL
THETA2 = NULL
accept1 = 0
accept2 = 0
S = 10000
theta1_s = 0
theta2_s = 0
for (s in 1:S) {
  
  ## propose and update theta1
  theta1_proposal = rnorm(1, mean = theta1_s, .5)
   log.r = logPosterior(theta1_proposal, theta2_s) - 
     logPosterior(theta1_s, theta2_s)
   
   if(log(runif(1)) < log.r)  {
    theta1_s = theta1_proposal
    accept1 = accept1 + 1 
   }
   
   THETA1 = c(THETA1, theta1_s)
   
   ## propose and update theta2
    theta2_proposal = rnorm(1, mean = theta2_s, .5)
   log.r = logPosterior(theta1_s, theta2_proposal) - 
     logPosterior(theta1_s, theta2_s)
   
   if(log(runif(1)) < log.r)  {
    theta2_s = theta2_proposal
    accept2 = accept2 + 1 
   }
   
   THETA2 = c(THETA2, theta2_s)
   
}

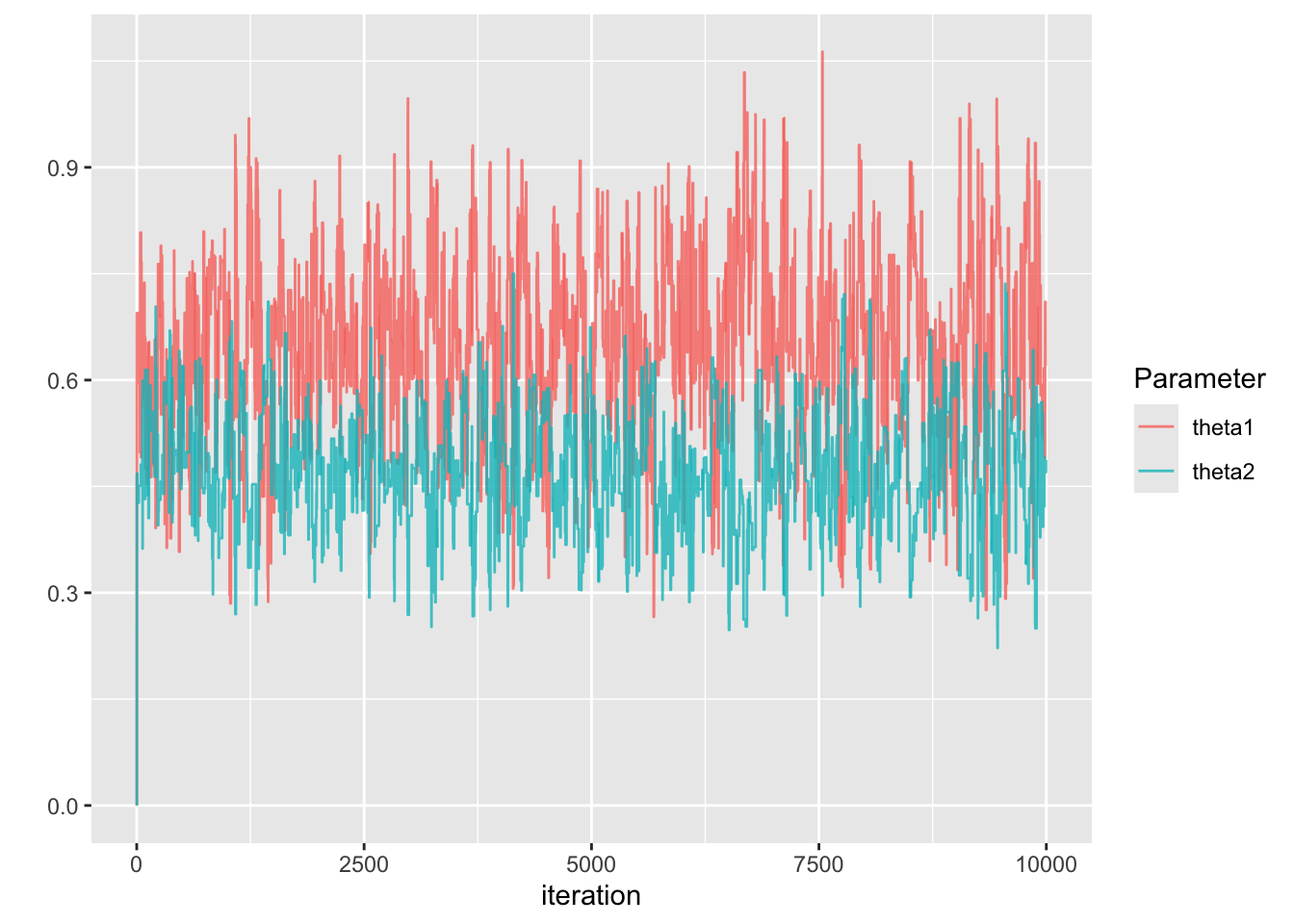
Parameter Posterior Mean 95% CI
\(\theta_1\) 0.65 (0.39, 0.9)
\(\theta_2\) 0.48 (0.3, 0.63)

Compare to lm:

fit = lm(mercury ~ weight, data = bass)
summary(fit)

Call:
lm(formula = mercury ~ weight, data = bass)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.71933 -0.41388 -0.09201  0.33615  2.14220 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.63868    0.08035   7.948 2.56e-13 ***
weight       0.48181    0.05572   8.647 3.93e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6361 on 169 degrees of freedom
Multiple R-squared:  0.3067,    Adjusted R-squared:  0.3026 
F-statistic: 74.77 on 1 and 169 DF,  p-value: 3.929e-15

Why does it work?

Ergodic theorem

Under what conditions does Metropolis-Hastings MCMC work?

Ergodic theorem: If \(\{\theta^{(1)}, \theta^{(2)}, \ldots \}\) is an irreducible, aperiodic and recurrent Markov chain, then there is a unique probability distribution \(\pi\) such that as \(s \rightarrow \infty\),

  • \(Pr(\theta^{(s)} \in \mathcal{A}) \rightarrow \pi(\mathcal{A})\) for any set \(\mathcal{A}\);

  • \(\frac{1}{S} \sum g(\theta^{(s)}) \rightarrow \int g(x) \pi(x) dx\).

Definitions

stationary distribution

\(\pi\) is called the stationary distribution of the Markov chain because if \(\theta^{(s)} \sim \pi\) and \(\theta^{(s+1)}\) is generated from the Markov chain starting at \(\theta^{(s)}\), then \(Pr(\theta^{(s+1)} \in \mathcal{A}) = \pi(\mathcal{A})\).

irreducible

A chain is reducible if the state-space can be divided into non-overlapping sets (due to some \(J\)). In practice, the proposal \(J(\theta^* | \theta^{(s)})\) needs to let us go from any value of \(\theta\) to any other, eventually.

aperiodic

We want our Markov chain to be aperiodic. A value \(\theta\) is said to be periodic with period \(k>1\) if it can only be visited every \(k\)th iteration. A Markov chain without periodic states is aperiodic.

recurrent

A value \(\theta\) is recurrent if we are guaranteed to return to it eventually.

Diagnostics

MCMC Vocabulary

  • autocorrelation: how correlated consecutive values in the Markov chain are. Mathematically, we compute the sample autocorrelation between elements in the sequence that are \(t\) steps apart using

\[ \text{acf}_t(\boldsymbol{\phi}) = \frac{\frac{1}{S - t} \sum_{s = 1}^{S-t} (\phi_s - \bar{\phi})(\phi_{s+t} - \bar{\phi})} {\frac{1}{S-1} \sum_{s = 1}^S (\phi_s - \bar{\phi})^2} \] where \(\boldsymbol{\phi}\) is a sequence of length \(S\) and \(\bar{\phi}\) is the mean of the sequence. Practically, we use acf function in R. Example:

acf(THETA1, plot = FALSE)

Autocorrelations of series 'THETA1', by lag

    0     1     2     3     4     5     6     7     8     9    10    11    12 
1.000 0.913 0.845 0.786 0.735 0.691 0.650 0.615 0.584 0.554 0.528 0.502 0.479 
   13    14    15    16    17    18    19    20    21    22    23    24    25 
0.458 0.436 0.418 0.400 0.384 0.370 0.354 0.339 0.322 0.302 0.288 0.276 0.264 
   26    27    28    29    30    31    32    33    34    35    36    37    38 
0.252 0.242 0.232 0.220 0.208 0.198 0.190 0.181 0.171 0.162 0.155 0.145 0.135 
   39    40 
0.124 0.113

The higher the autocorrelation, the more samples we need to obtain a given level of precision for our approximation. One way to state how precise our approximation is, is with effective sample size.

  • effective sample size (ESS): intuitively this is the effective number of exact samples “contained” in the Markov chain (see Betancourt 2018). For further reading on ESS, see the stan manual. In practice we use coda::effectiveSize() function to compute. Example:
library(coda)
effectiveSize(THETA1)
    var1 
302.4272

More precisely, the effective sample size (ESS) is the value \(S_{eff}\) such that

\[ Var_{MCMC}[\bar{\phi}] = \frac{Var[\phi]}{S_{eff}}. \] In words, it’s the number of independent Monte Carlo samples necessary to give the same precision as the MCMC samples. For comparison, recall \(Var_{MC}[\bar{\phi}] = Var[\phi]/S\)

  • Stationarity is when samples taken in one part of the chain have a similar distribution to samples taken from other parts of the chain. Intuitively, we want the particle to move from our arbitrary starting point to regions of higher probability\(^*\), then we will say it has achieved stationarity.

Traceplots are a great way to visually inspect whether a chain has converged, or achieved stationarity. In the traceplot from the previous lecture, we can see that samples from the beginning of the chain look very different than samples at the end for delta = 0.1.

\(^*\) recall that probability is really a volume in high dimensions of parameter space, and so it is not enough for a pdf to evaluate to a high value, there must also be sufficient volume.

  • Mixing: how well the particle moves between sets of high probability. Some might refer to this as how well the particle sojourns across the “typical set” (regions of high probability).