Bayesian model averaging

Author

Dr. Alexander Fisher

Motivation

Consider the standard regression problem,

\[ Y | \beta, \sigma^2 \sim N_n(X\beta, \sigma^2 I_n) \] where each term is of typical dimension,

  • \(Y \in \mathbb{R}^n\) vector of observations,
  • \(X \in \mathbb{R}^{n \times p}\) matrix of predictors,
  • \(\beta \in \mathbb{R}^p\) vector of coefficients,
  • \(\sigma^2 \in \mathbb{R}\), and
  • \(I_n \in \mathbb{R}^{n \times n}\).

Often, when we have many covariates, i.e. \(p\) is large, we believe that some do not really explain \(Y\). A particular subset of the explanatory variables is termed a model of \(Y\). Since each explanatory variable belongs in the model, or does not, there are \(K = 2^p\) total models we can consider.

For notational convenience, let \(M_1, \ldots, M_{K}\) be the models under study.

Important

For even modestly large \(p\), such as \(p=64\) in the example below, there are more possible models \(2^{64} \approx 1.8 \times 10^{19}\) than there are grains of sand on earth (about \(7.5 \times 10^{18}\)).

For this reason, we will never be able to sample a substantial proportion of all the models.

There are many different questions one might answer with a regression model. Sometimes, the model itself is of interest i.e. we wish to select a single model \(M_j\). Other times, we may care about estimating a particular coefficient \(\beta_i\) to understand how a single predictor relates to \(Y\). Alternatively, we may really care about making predictions for new data.

These tasks are not mutually exclusive, but might direct our approach differently.

In particular, if we are interested in prediction, or estimating a particular coefficient, then it’s important to realize that estimates such as \(\hat{\beta}\) or a function thereof, \(\hat{Y} = X \hat{\beta}\) are implicitly conditioned on a specific model.

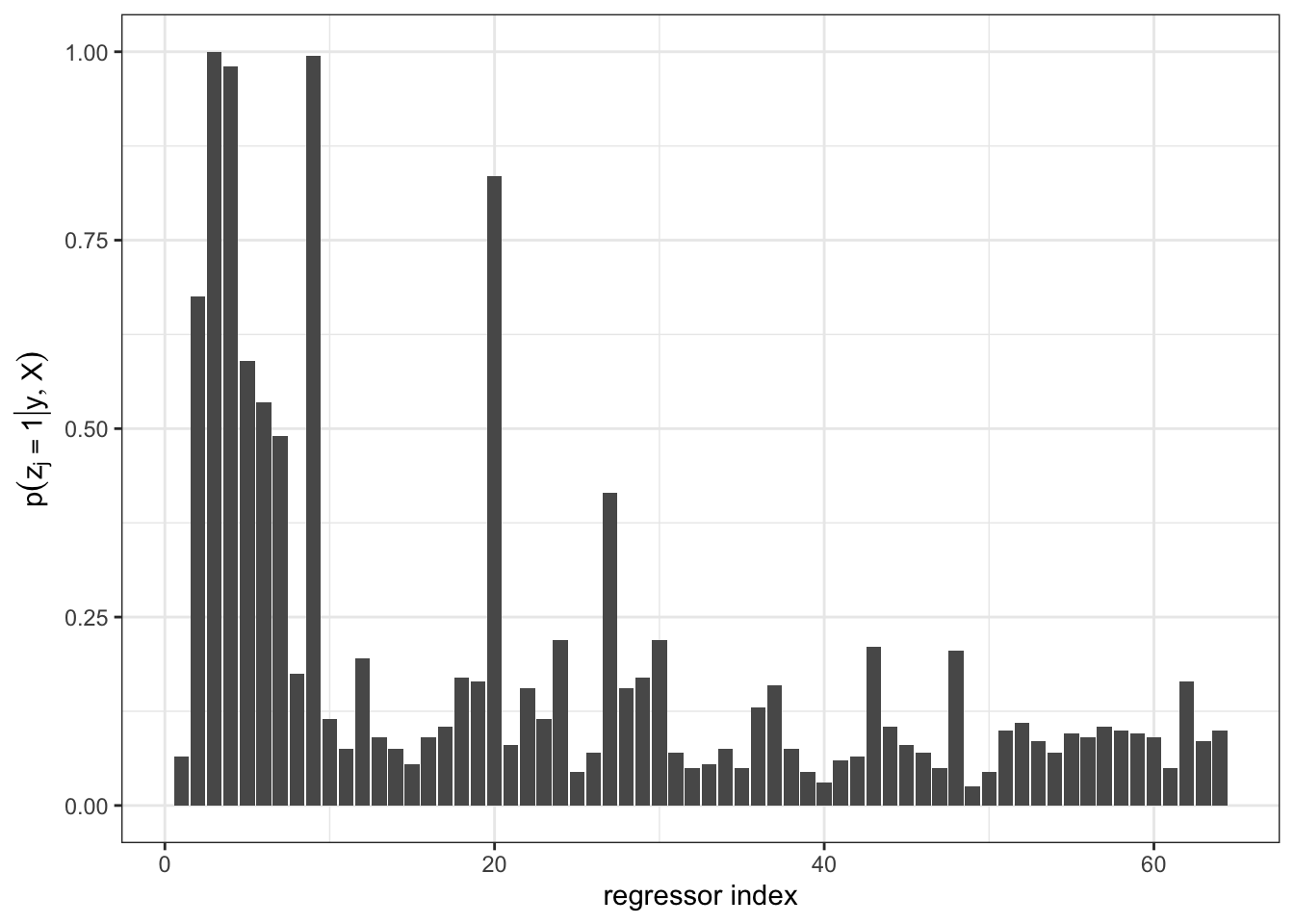
  • How can we address uncertainty in the model itself?

Model averaging setup

Let \(z \in \mathbb{R}^p\) be a vector of indicator variables \(z_1, \ldots, z_p\), where \(z_j = 1\) means the \(j\)th predictor is in the model, and \(z_j = 0\) means it is not. Conceptually, \(z\) tells us which regression coefficients are non-zero.

\[ y_i = z_1 \beta_1 x_{i, 1} + \ldots + z_p \beta_p x_{i,p} + \epsilon \]

where \(\epsilon \sim N(0, \sigma^2)\).

In matrix form,

\[ Y|\beta, z, \sigma^2 \sim N_n(XZ\beta, \sigma^2 I_n) \]

where \(Z = z I_p\) is a diagonal matrix.

Note

Each separate “model” \(M\) is equivalent to a different vector \(z\).

Once we’ve setup our likelihood to explicitly condition on the model, \(z\), we continue our usual Bayesian practice: we make inferences about all unknowns: \(\beta, \sigma^2\), and \(z\).

Now, however we can differentiate between estimates of \(\beta\) conditional on a model,

\[ E[\beta | y, z] = \int \beta p(\beta | y, z) d\beta \]

versus estimates of \(\beta\) that account for model uncertainty:

\[ \begin{aligned} E[\beta | y] = \sum_{z} \int \beta p(\beta, z | y) d\beta \end{aligned} \]

Complete Bayesian model

Data generative model:

\[ Y|\beta, z, \sigma^2 \sim N_n(X_z\beta_z, \sigma^2 I_n) \] Common prior specification:

\[ \begin{aligned} \beta_z | \sigma^2 &\sim N_z \left(0, g \sigma^2 (X_z^TX_z)^{-1}\right)\\ 1/\sigma^2 &\sim \text{gamma}(\frac{\nu_0}{2}, \frac{\nu_0}{2} \sigma_0^2)\\ p(z_i = 1) &= \frac{1}{2} \text{ for all i} \end{aligned} \] where \(g\) is some fixed constant and \(\beta_z\) is the set of \(\beta\) corresponding to non-zero entries of \(z\) (\(X_z\) is constructed similarly). The prior on \(\beta\) is known as Zellner’s \(g\) prior 1. The \(g\) prior is mathematically convenient and leads to nice marginal distributions for our Gibbs sampler.

Where does the prior variance of \(\beta\) come from? Recall: \(Var[\hat{\beta}_{OLS}] = \sigma^2 (X^TX)^{-1}\). So a priori we expect the variance of \(\beta\) to look like the OLS variance and \(g\) controls the weight of this prior variance (or \(1/g\) controls the weight of the precision). Small \(g\) implies more prior precision relative to the data.

  • Question: what should \(g\) be equal to for unit precision?

Beta

\[ \beta_z | X_z, \sigma^2, y \sim N_z\left( A^{-1}b, A^{-1} \right) \] where \(A^{-1} = \sigma^2 \left( \frac{g}{g+1}\right)(X_z^TX_z)^{-1}\) and \(b = \frac{1}{\sigma^2} X_z^Ty\).

We can simplify the full conditional notation,

\[ \beta_z | X_z, \sigma^2, y \sim N_z\left( \left(\frac{g}{g+1}\right)\hat{\beta}_{z(OLS)},~ \left(\frac{g}{g+1}\right) \sigma^2 \left[X_z^TX_z\right]^{-1} \right) \]

sigma-squared

We can integrate out \(\beta\) analytically, for a more efficient sampler,

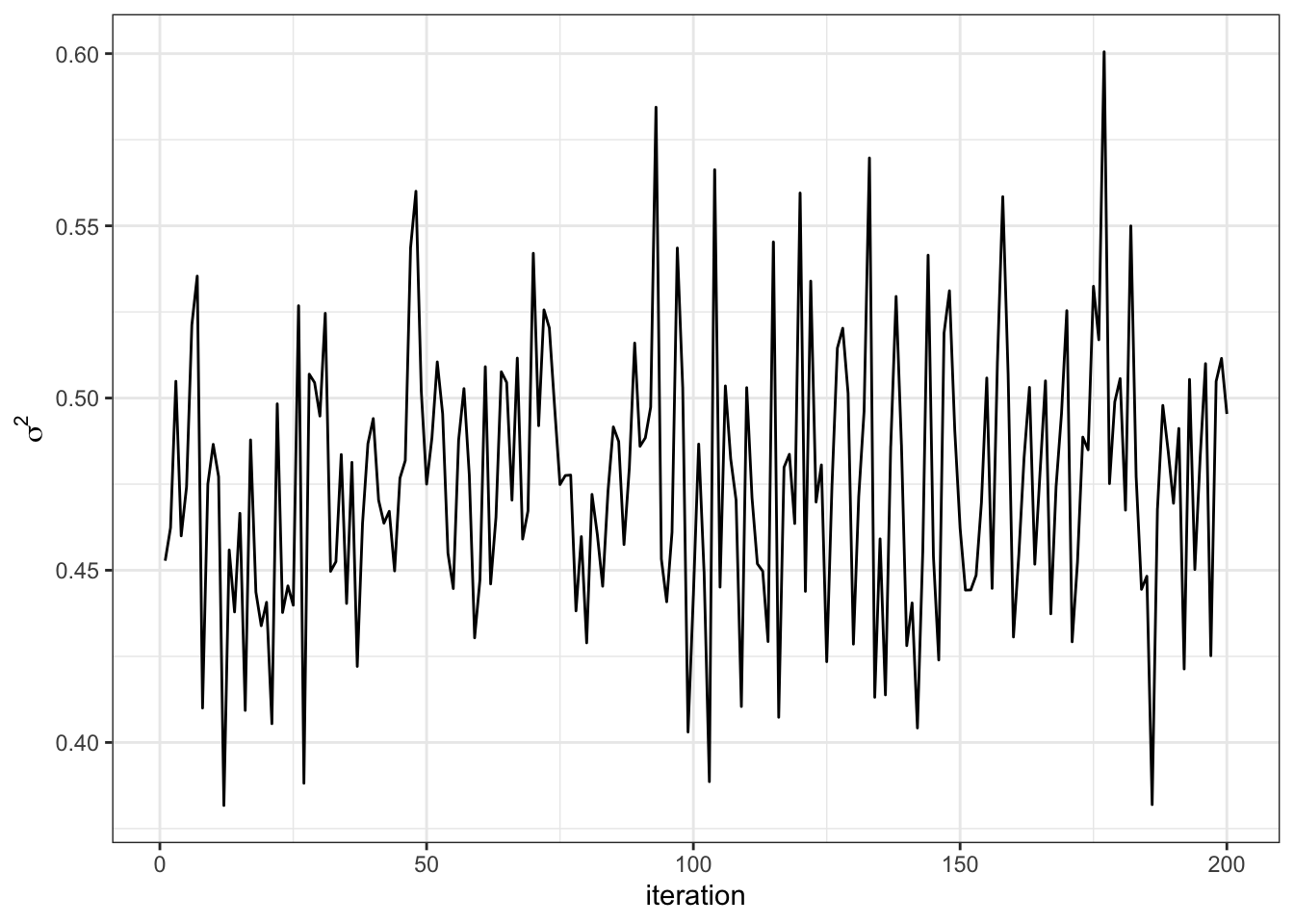
\[ 1/\sigma^2 | X_z, y \sim \text{gamma}([\nu_0 + n]/2, [\nu_0 \sigma_0^2 + SSR_g^z]/2) \] where \(SSR_g^z = y^T(I - \frac{g}{g+1} X_z (X_z^T X_z)^{-1} X_z^T)y\)

z

\[ z_j \sim \text{binary}(o_j/(1 + o_j)) \] where \(p_j\) is the probability that \(z_j = 1\), and is given by

\[ o_j = \frac {Pr(z_j = 1 | y, X, z_{-j})} {Pr(z_j = 0 | y, X, z_{-j})} = \frac{p(y|X, z_{-j}, z_j = 1) p(z_j = 1)} {p(y|X, z_{-j}, z_j = 0) p(z_j = 0)} \] See page 165 of the book for details on how to compute the marginal likelihood \(p(y|X, z)\).

Example: Diabetes

This example comes from Hoff Ch 9.

The data below contains our outcome variable, diabetes progression (first column) and 64 predictors. This example and data set appeared on a previous homework.

load libraries 
library(tidyverse)
library(mvtnorm)
library(latex2exp)
library(coda)
data load and setup 
yX.diabetes.train<-dget(url("https://sta360-fa24.github.io/data/yX.diabetes.train"))

X = yX.diabetes.train[,-1]
y = yX.diabetes.train[,1]
useful functions 
# log-probability of y given x
lpyx = function(y, X, g=length(y), 
                nu0=1, s20 = try(summary(lm(y~1+X))$sigma^2, silent = TRUE)) {
  n=nrow(X)
  p=ncol(X)
  if(p==0) {
    Hg = 0
    s20 =mean(y^2)
  }
  if(p>0) {
    Hg = (g / (g + 1)) * X %*% solve(t(X) %*% X) %*% t(X)
  }
  
  SSRg = t(y) %*% (diag(1, nrow = n) - Hg) %*%y
  -.5 *(n *log(pi) + p * log(1 + g) + (nu0 + n) * log(nu0 *s20 + SSRg)- nu0 *log(nu0 *s20)) +
    lgamma((nu0 + n) / 2) - lgamma(nu0 / 2
    )
}

SSR = function(y, X, g = length(y)) {
  n=nrow(X)
  p=ncol(X)
  Hg = (g/(g+1)) * X %*% solve(t(X) %*% X) %*% t(X) 
  return(t(y) %*% (diag(1,nrow=n) - Hg) %*% y)
}

getVarianceBeta = function(X, s2, g = length(y)) {
  (g / (g+1)) * s2 * solve(t(X) %*% X)
}

getOLS_mean = function(y, X, varBeta, g = length(y)) {
  varBeta %*%  t(X) %*% y
}
MCMC 
# setup
S = 200 # num iterations

# fixed quantities
nu0 = 1
sigma02 = 1
alpha_n = (nu0 + n)/2
beta_const = nu0 * sigma02
g = length(y)
# objects to fill
Z = matrix(NA, S, p)
BETA = matrix(NA, S, p)
SIGMA2 = matrix(NA, S, 1)

## starting values ##
z = rep(1, ncol(X))
lpy.c = lpyx(y , X[,z==1, drop=FALSE])
gamma = 1
## Gibbs sampler
for(s in 1:S) {
  # update z
  for (j in sample(1:ncol(X))) {
    zp = z
    zp[j] = 1 - zp[j]
    lpy.p = lpyx(y, X[,zp==1, drop = FALSE])
    r = (lpy.p - lpy.c) * (-1)^(zp[j]==0)
    z[j] = rbinom(1, 1, 1 / (1+exp(-r)))
    if(z[j] == zp[j]) {
      lpy.c = lpy.p
    }
  }
  Z[s,] = z
  
  ## update sigma^2
  s2 = 1 / rgamma(1, alpha_n, (beta_const + 
                                 SSR(y, X[,z==1, drop = FALSE]))/2)
  
  SIGMA2[s] = s2
  
  ## update beta
  
  varBeta = getVarianceBeta(X[,z==1, drop = FALSE], s2)
  meanBeta = getOLS_mean(y, X[,z==1, drop = FALSE], varBeta / s2)
  
  beta = rmvnorm(1, mean = meanBeta,
                 sigma = varBeta)
  BETA[s,z==1] = beta
}

trace plots

Code 
data.frame(sigma2 = SIGMA2[,1]) %>%
  ggplot(aes(x = 1:S)) +
  geom_line(aes(y = sigma2)) +
  theme_bw() +
  labs(x = "iteration", y = TeX(r'($\sigma^2$)'))

Code 
data.frame(beta2 = BETA[,2]) %>%
  mutate_at(1, ~ replace(., is.na(.), 0)) %>%
  ggplot(aes(x = 1:S)) +
  geom_line(aes(y = beta2)) +
  theme_bw() +
  labs(x = "iteration", y = TeX(r'($\beta_2$)'))

effective size

apply(Z, 2, effectiveSize)
       V1        V2        V3        V4        V5        V6        V7        V8 
200.00000 122.61862   0.00000 103.73609  46.31771  27.11704  36.39864 103.84635 
       V9       V10       V11       V12       V13       V14       V15       V16 
200.00000 200.00000 200.00000 131.97829 200.00000 200.00000 200.00000 105.30279 
      V17       V18       V19       V20       V21       V22       V23       V24 
200.00000 109.46251 200.00000 125.03977 200.00000 133.38260 141.21845 200.00000 
      V25       V26       V27       V28       V29       V30       V31       V32 
200.00000 200.00000  87.26784 156.01952 200.00000 200.00000 200.00000 200.00000 
      V33       V34       V35       V36       V37       V38       V39       V40 
200.00000 200.00000 200.00000 157.92121 200.00000 200.00000 200.00000 159.02378 
      V41       V42       V43       V44       V45       V46       V47       V48 
200.00000 154.07992  86.32241 200.00000 200.00000 200.00000 200.00000 124.12176 
      V49       V50       V51       V52       V53       V54       V55       V56 
200.00000 200.00000 200.00000 200.00000  98.08846 200.00000 200.00000 112.44715 
      V57       V58       V59       V60       V61       V62       V63       V64 
147.64897 200.00000 200.00000 200.00000 200.00000 117.52886 200.00000 200.00000 
apply(SIGMA2, 2, effectiveSize)
 V1 
200
Code 
yX.diabetes.test<-dget(
  url("https://sta360-fa24.github.io/data/yX.diabetes.test"))
Xtest = yX.diabetes.test[,-1]
ytest = yX.diabetes.test[,1]

betaHat = as.vector(colSums(BETA, na.rm = TRUE) / S)
yHat = Xtest %*% betaHat

data.frame(yHat, ytest) %>%
  ggplot(aes(x = yHat, y = ytest)) +
  geom_point() +
  geom_abline(intercept = 0, slope = 1) +
  theme_bw() +
  labs(x = TeX(r'($\hat{y}$)'), y = "y")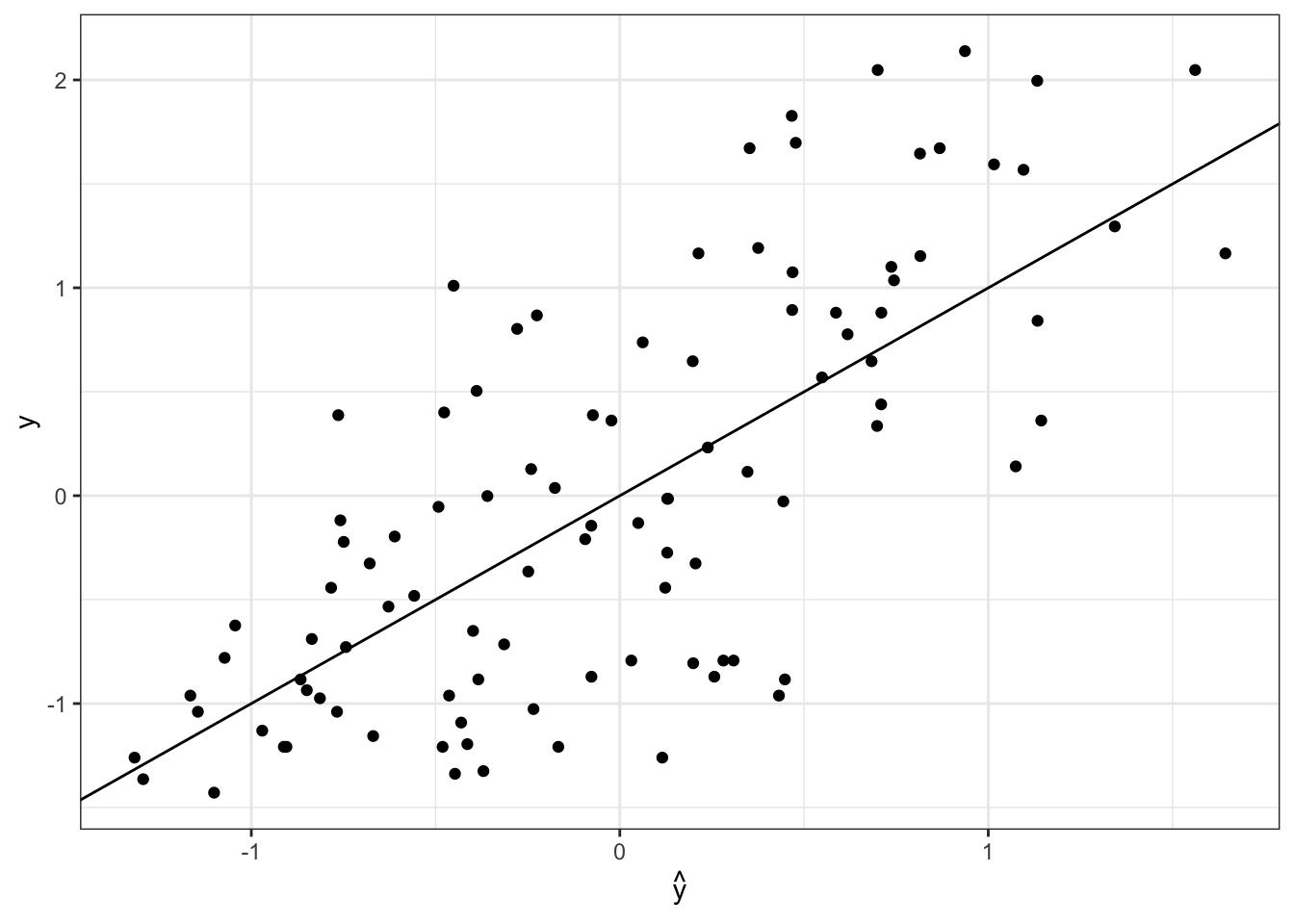

The predictive sum of squared error is

sum((yHat - ytest)^2)
[1] 45.2647

Compare this to the predictive sum of squared error from ridge regression on the homework.

Footnotes

  1. Zellner, Arnold. “On assessing prior distributions and Bayesian regression analysis with g-prior distributions.” Bayesian inference and decision techniques (1986).↩︎